◆イントロダクション
おじいちゃん、物理の「解析力学」で「ラグランジュの未定乗数法」っていうワードが出てきたけど、よく意味が分からないの!


「ラグランジュの未定乗数法」っていうのは、
束縛条件のもとで最適化を行うための数学(解析学)的な方法である。いくつかの変数に対して、いくつかの関数の値を固定するという束縛条件のもとで、別のある1つの関数の極値を求めるという問題を考える。
(Wikipediaから引用)

簡単に言うと、「複雑な制限があるとき、物体の動きを予測するための、裏ワザというか最終兵器」だよ。
◆詳しく説明
ひまりちゃんが、かたむいた道の上で車を運転しています。
あなたはそれを眺めています。

上から見るとこんな感じです。↓
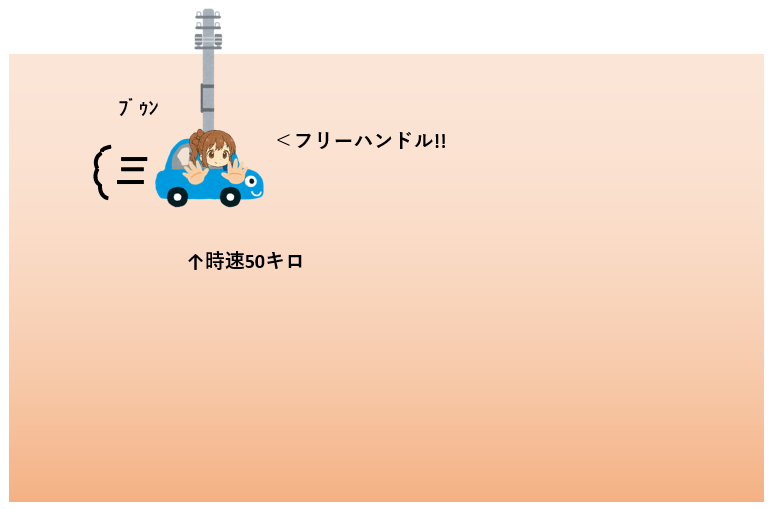
ひまりちゃんは、速さ50kmで電柱を通り過ぎました。
そして、それと同時に、ハンドルとペダルから手と足をはなしました。
(よい子はやっちゃダメですよ。)
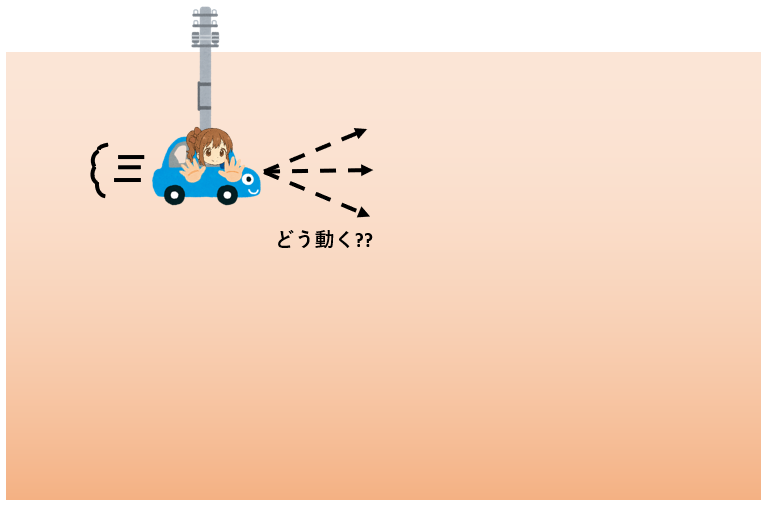
すると、車はどういう動きをするでしょうか??
こんなとき、車の動きを予測するために、「ニュートンの運動方程式」というアイテムが使えます。
いまから350年くらい前にニュートンさんという偉い人が発見した秘密アイテムです。

あなたは「ニュートンの運動方程式」を使って、「ひまりちゃんは5秒後にココにいる!」と予想しました。
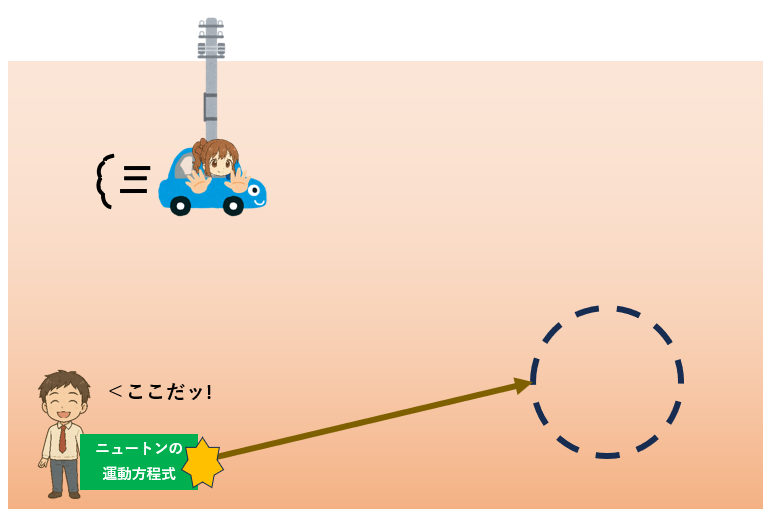
さてどうなる?
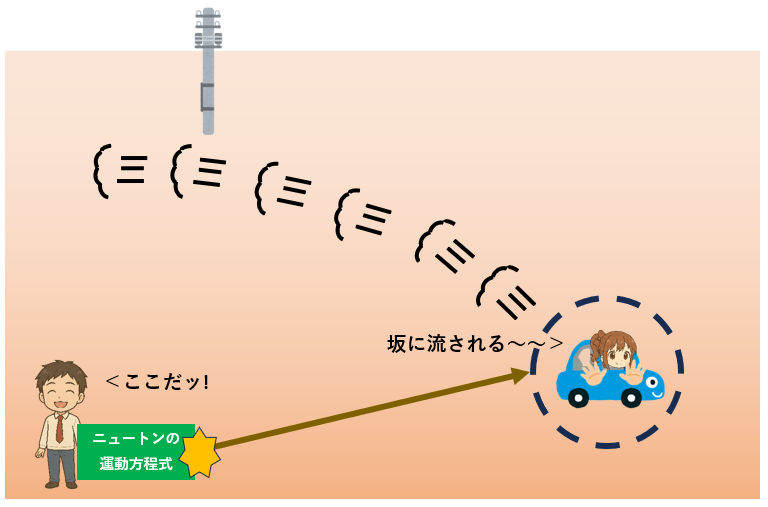
ね、確かにそうなったでしょ。
では、ひまりちゃんが丸い形に敷かれたレールの上を走っている場合はどうでしょう。
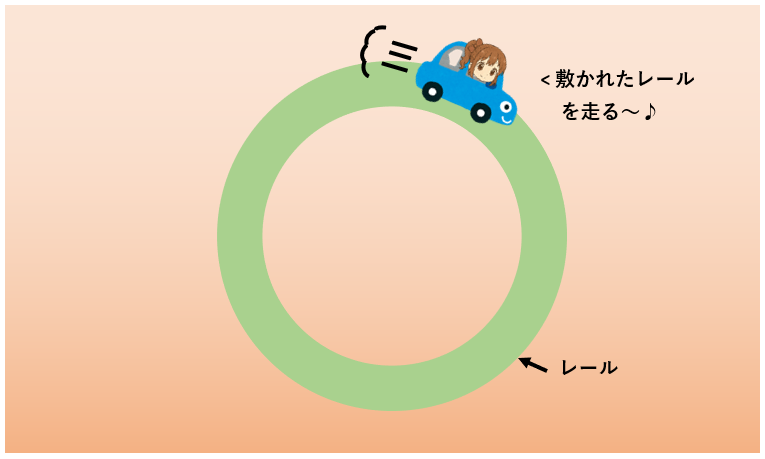
あなたは「ニュートンの運動方程式」を使おうとしましたが、なかなかうまくいきません。
(理由はコースが丸いからです。)
そこで、「ニュートンの運動方程式」のパワーアップ版であるアイテム、「ラグランジュの運動方程式」というアイテムを取り出しました。
いまから300年くらい前にラグランジュさんというすごい人が発明したスーパーアイテムです。


あなたは「ラグランジュの運動方程式」を使って、「ひまりちゃんは10秒後にココにいる!と予想しました。
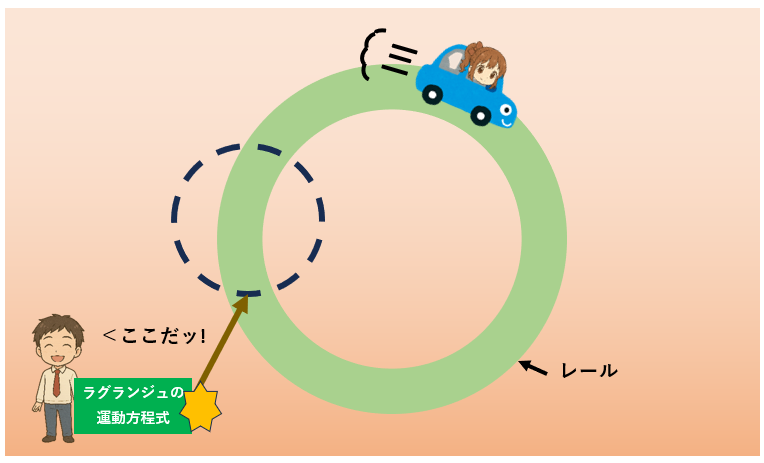
さてどうなる?
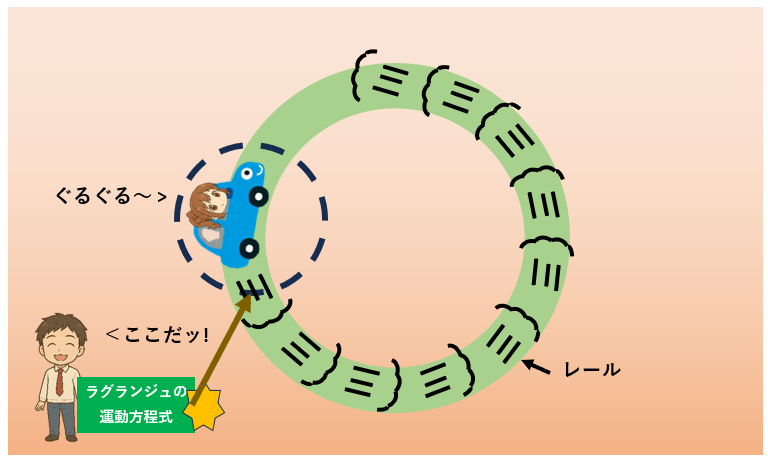
ね、確かにそうなったでしょ。
ではでは、もっともっと難しい例も考えてみましょう。
レールはとっぱらって、ひまりちゃんは自由に運転できるとします。
ひまりちゃんはハンドルも操作するし、アクセルやブレーキも踏むとします。
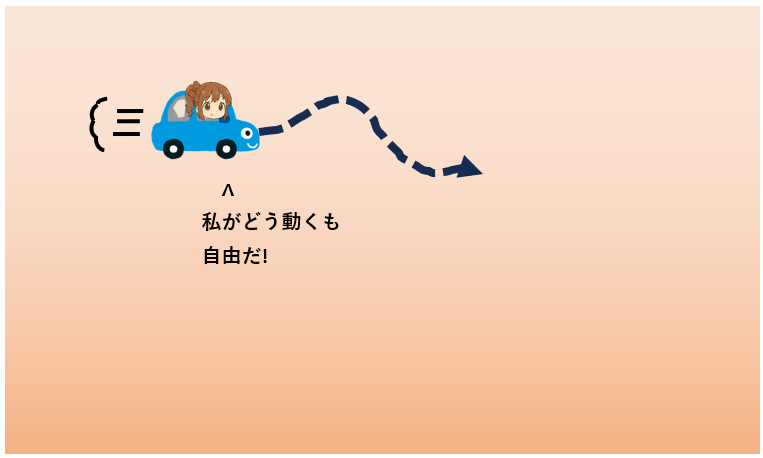
もはやなんの制約もなく動き放題? いや、じつは制約はあります。
想像してみると、自動車って、東をむいたまま北には進めませんよね。
東を向いた状態から北に移動するためには、ちょっと回るようにして方向転換しないといけません。
そういう意味で、動き方には制約はあります。
あくまで車の機能上できる動きの範囲では自由に動かせますよ、ということです。
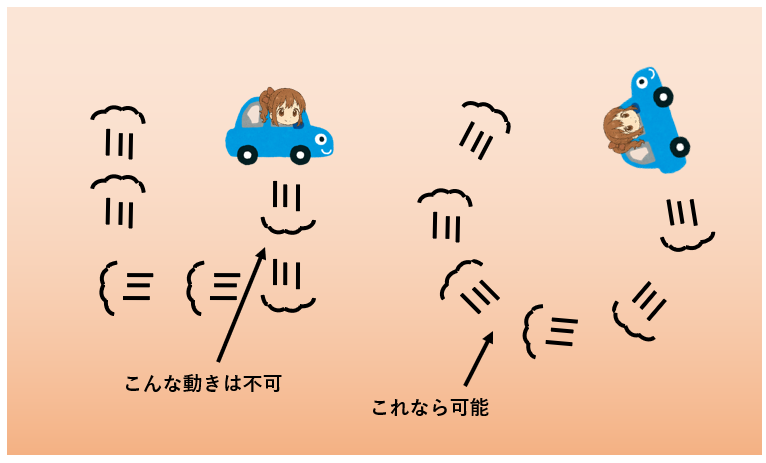
これじゃあ、もう、ひまりちゃんの車の動きを予想することなんてできない?
いや、でも、ひまりちゃんが、何時何分に、ハンドルをどう切るかとか、アクセルやブレーキをどう踏むかとかを、あらかじめぜんぶあなたに教えてくれてさえいたら、原理的には、ものすごく頑張って計算すれば、ひまりちゃんの車の動きを予想できるはずです。

でも、条件が複雑すぎて、「ラグランジュの運動方程式」だけでは不可能です。
そこであなたがとりだした最終兵器が、「ラグランジュの未定乗数法」です。

このアイテムの万能性はすごいです。
「ラグランジュの運動方程式」に「ラグランジュの未定乗数法」をあわせれば、
複雑な条件下であっても、ひまりちゃんの車の動きを予想することが可能です。
あなたは「ラグランジュの運動方程式」と「ラグランジュの未定乗数法」の合わせ技で、「ひまりちゃんは25秒後にココにいる!」と予測しました。
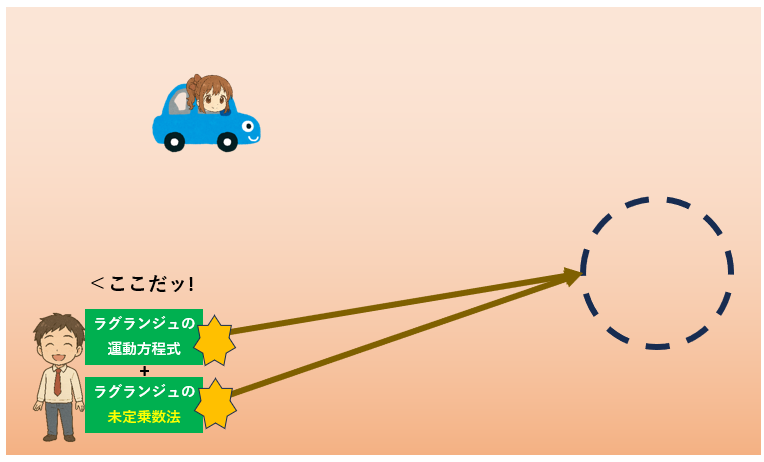
さてどうなる?
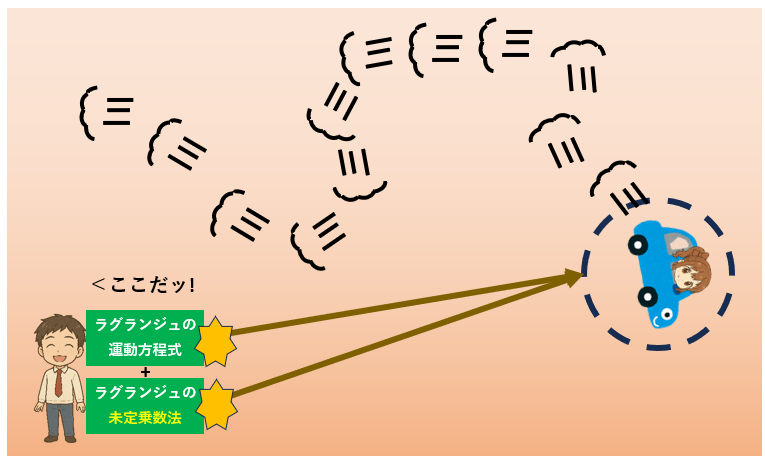
ね、確かにそうなったでしょ。
◆つまり?
…
上のお話のとおり、「ラグランジュの未定乗数法」は「複雑な条件下での物体の動きを予測するためのアイテムであり、最終兵器」です。
一部の人たちの間では、「強すぎる」「全部これで解決するんじゃない?」といわれるほどのスグレモノです。
ただし、属性としては、「物理のアイテム」ではなく、「数学のアイテム」です。
「ラグランジュの運動方程式」という「物理のアイテム」と、「ラグランジュの未定乗数法」という「数学のアイテム」を合わせることによって、とてつもない威力を発揮するのです。
よかったら覚えておいてください。
なんか、わかったような? 気がする!

◆まとめ
「ラグランジュの未定乗数法」っていうのは、
「複雑な制約条件がある場合でも物体の動きを正確に予想できる超有能アイテム」のことなんだね♪
