「一般化座標」って何

　

◆イントロダクション

　

◆詳しく説明

ボールが飛んでいます。
あなたはそれを見ています。

いま、ボールは空中を真横にまっすぐ飛んでおり、飛んでいる途中で速さは変わらないとします。
あなたは、このボールの運動（＝動き方）を、たくや先生に伝えないといけません。

ただし、その時に絵を使ってはいけません。
なぜなら、たくや先生は絵 恐怖症だからです。

あくまで言葉だけで、伝えないといけないのです。
あなたはどう言いますか?

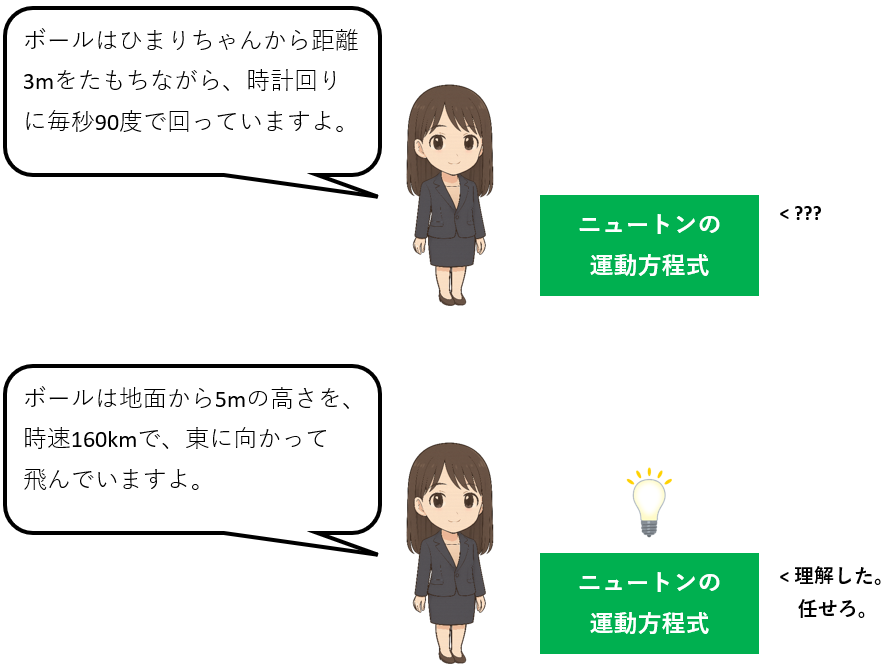
「ボールは地面から5mの高さを、時速160kmで、東に向かって飛んでいますよ。」
こう伝えればいいですね。

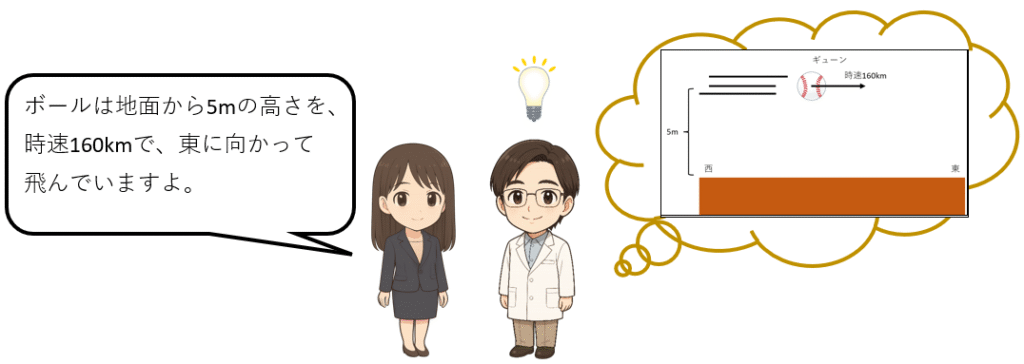
要は、
「速度は横に時速160km、縦に0km
　高さ（＝縦の位置）はずっと5m」
ということです。

つまり、「タテ、ヨコ」を使って伝えているわけです。
このような伝え方を、「直線直交座標」といいます。（重要!）

では、こんどは、ボールがひまりちゃんの周りをぐーるぐーると回っている場合はどうでしょうか?
この場合、たくや先生に伝えるにはどうすればいいでしょうか。

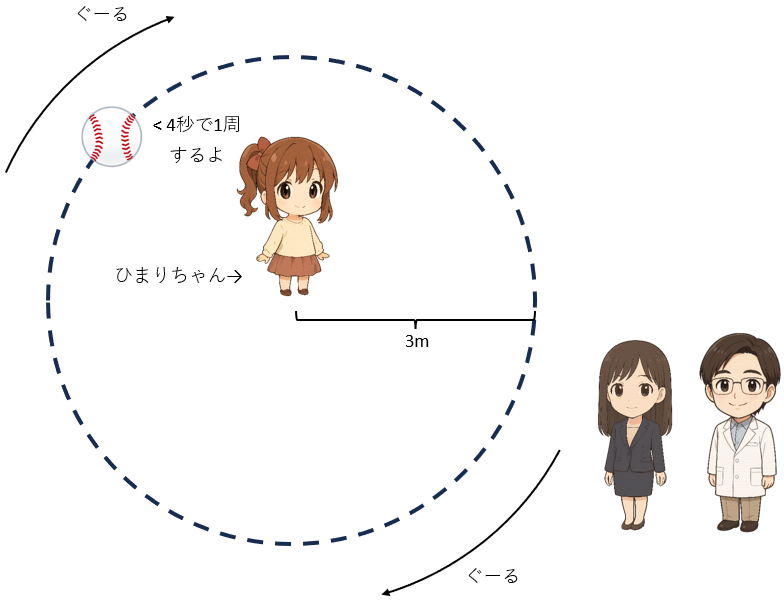
「ボールはひまりちゃんから距離3mをたもちながら、
　時計回りに毎秒90度で回っていますよ」
のように伝えればよさそうです。

要は、「ひまりちゃんからの距離と、角度」を使って伝えているわけです。
このような伝え方を、「極座標系」といいます。（重要!）

「直線直交座標系」と「極座標系」のほかにも、実はいろんな座標系があります。

たとえば、「タテ、ナナメ」で伝える座標系とか。

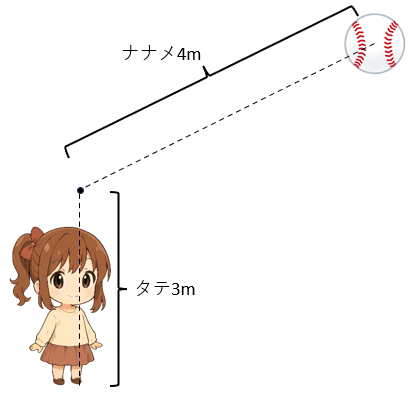
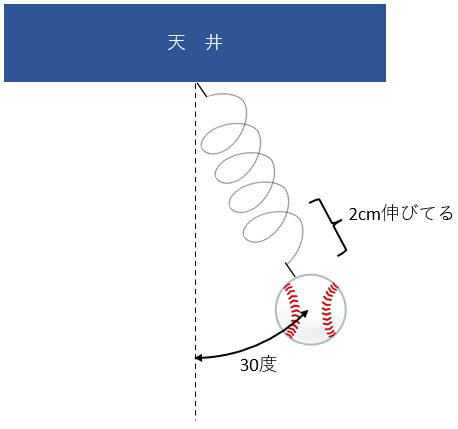
たとえば、「ばねの伸びた長さと、ばねの角度」で伝える座標系とか。

まだまだ、ありますよ。

こんなふうに、直線直交座標系以外の座標系を、ぜんぶぜーんぶ含めた、いろんな座標系を、「一般化座標」というんですよ。

「一般化」は、「直線直交座標系だけに限定しない、一般の」という意味ですね。

ところで、物理学では、物体の動きを予測するために、「ニュートンの運動方程式」というアイテムがあるのをご存知ですか?

「ニュートンの運動方程式」は、350年前くらいに、イギリス人のニュートンという人が編み出した、物体の動きを予測するための秘密アイテムです。

しかし、この秘密アイテム、じつはちょっと融通がきかなくて…「直線直交座標系」の話し方で情報を渡してやらないと、ウンともスンとも使えないんです!

なんて困った仕様でしょう!
「一般化座標系」では使えないんです!

これでは使い勝手が悪い! ということで、ニュートンの何十年もあとで、フランス人のラグランジュという人が、もっと便利なスーパーアイテム、その名も「ラグランジュの運動方程式」を開発しました。

「ラグランジュの運動方程式」は、「一般化座標」で情報を与えても、動いてくれるんですよ。

　

◆つまり?

上記のお話しを整理します。

• 「位置の表し方」のことを「座標」といい、「座標」の種類には「直線直交座標系」「極座標系」「斜交座標系」など色々ある。
• それらぜんぶの座標系をまとめて「一般化座標」とよぶ。
• 「ニュートンの運動方程式」は「直線直交座標系」で情報を渡してやれば動くけど、それ以外の「一般化座標系」では動かない。

要は、一般化座標は自由な座標の表し方なんだな、ということだけ覚えておいてください。

　

◆まとめ